王先生是一位收藏家,他收集了非常多有名的雕像。某天,为了美观,他想要将收藏台上的雕像按照某种方式重新摆放,由于雕像都有一定的重量,所以他决定雇用一位年轻人,小明,來帮忙搬雕像。
王先生收藏的雕像目前是以随机的方式放在收藏台上,收藏台的位置由左至右成一列排开,编号依序为1, 2,..., n ,每个收藏台上放置一个雕像,而收藏台i (1 ≤ i ≤ n) 上目前放的雕像编号为 Si,其高度为 hi 公分,重量为 wi 公斤。王先生要求小明依照下列方式去重新摆放雕像: (a) 搬动过程中,一次只能搬一个雕像,而每个收藏台可暂时放置 0个、1 个、或多个雕像。 (b) 完成重新摆放之后需符合下列条件:- 每个收藏台上放置一个雕像。
- 雕像必须根据高度,由低至高从最左边的收藏台开始依序放置。
- 若任二雕像的高度相同时,则重量轻的雕像放置在左边。
- 若任二雕像高度和重量都相同时,则依照原先雕像的左右相对顺序來放置,也就是說原先在左边的雕像必须放置在左边。
为了节省搬运的距離,小明希望你替他写出一个程序,根据上述方式将雕像重新摆放在收藏台上且搬动的总距離为最短。本题假设任二相邻收藏台的距離为1 公尺。
以下为一个范例,假设有 5 个收藏台,雕像 Si (1 ≤ i ≤ 5) 的高度和重量以(hi, wi)表示,并依序为(5,20) ,(10,25) ,(78,40) ,(25,25) ,(5,15) 。一种搬动方式如图(a)所示,搬动的总距離为 12公尺,而另一种搬动方式如图(b)所示,搬动的总距離为8 公尺,是所有符合搬动方式中的最短距離。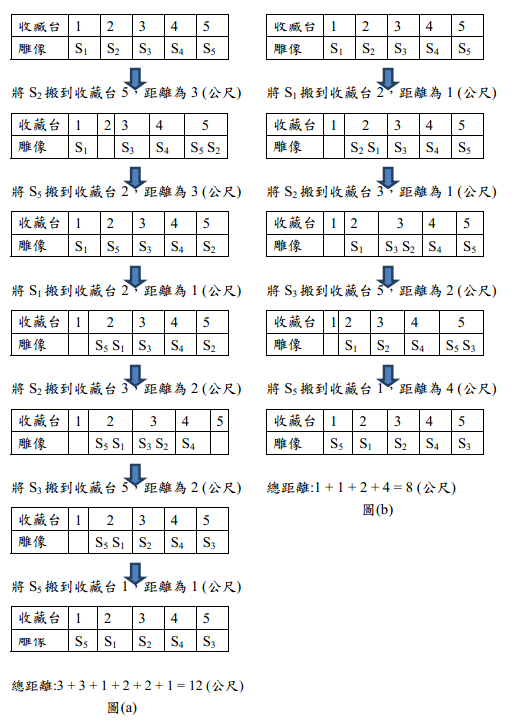
第一行有一个整數n,1≤ n≤ 10000,代表收藏台的个數。接下來的n 行,每行有兩个整數以空白隔开,其中第 i 行(1 ≤i ≤ n) 为目前放在收藏台i 上雕像Si 的高度hi( 单位为公分) 和重量wi( 单位为公斤) ,hi 和wi 都介于1 和65536 之间
输出一个整數,代表搬动雕像所需的最短总距離( 单位为公尺) 。
样例1:
5
5 20
10 25
78 40
25 25
5 15
样例2:
8
5 15
3 5
9 13
13 20
24 30
40 50
9 12
5 15
样例1:
8
样例2:
18
1≤ n≤ 10000
hi 和wi 都介于1 和65536 之间
TW一百学年度全国高级中学咨询学科能力竞赛决赛1
今天蒽的托人给我送来水果,
还是很开心的。
告别昨天,迷茫云烟,,
把不开心的都忘掉吧。
这个题我一开始觉得肯定要用冒泡啊什么的
一步一步来模拟过程,
在模拟的过程中加上距离,
不能用快排,因为这样体现不出过程,
就没法求距离了。(都怪例子坑了我)
事实证明我错了。
模拟过程相当复杂且不易想出比较好的思路。
当然应该也可以,
但正解应该是用快排,
那么如何求最短移动距离呢?
直接从结果入手来求呀!
然后可以写出排好序后的样例,
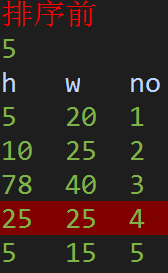
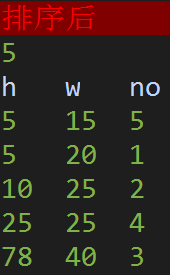
可以多试几组样例,
发现最终求得的最短移动距离恰等于移动前后各位置序号差的和。
(no代表序号)
所以就可以直接用快排,最后算结果就好了。
ac代码:
1 #include2 #include 3 #include 4 #include 5 #include 6 using namespace std; 7 8 int n,b[10002],t; 9 10 struct node{11 int h,w,no;12 }a[10002];13 14 bool cmp(node x,node y)15 {16 if(x.h >y.h ) return false;17 if(x.h y.w ) return false;19 if(x.w
如果你不开心,那我就把右边这个帅傻子分享给你吧, 你看,他这么好看,跟个zz一样看着你,你还伤心吗? 真的!这照片盯上他五秒钟就想笑了。 一切都会过去的。 时间时间会给你答案2333